Stuff

Links

Using Arrows for Dependency Handling

What is this about

Arrows are, like Monads or Monoids, a mathematical concept that can be used in the Haskell programming language. This post analyzes and explains a certain use case for Arrows, namely dependency tracking. But let’s begin with a quite unrelated quote from Jimi Hendrix.

Well my arrows are made of desire
From far away as Jupiter’s sulphur mines

Arrows are less common than Monads or Monoids (in Haskell code, that is), but they are certainly not harder to understand. This blogpost aims to give a quick, informal introduction to Arrows. As concrete subject and example, we use dependency handling in Hakyll.

The problem

Hakyll is a static site generator I use to run this blog. The principles behind it are pretty simple: you write your pages in markdown or something similar, and you write templates in html. Then, you render the pages with some templates using a configuration DSL.

In Hakyll, the rendering algorithm is more or less like this:

• Read a page from a file, say contact.markdown.
• Parse and render this page to HTML using pandoc.
• Do some further manipulations on the result.
• Render the result using a HTML template.
• Write the result to _site/contact.html.

The catch is, say _site/contact.html is “newer” than contact.markdown and the HTML templates. In this case, we do not want to do anything. Haskell lazyness will not help us a lot here, since we’re dealing with a lot of IO code.

Suppose we’re currently reading the page from a file. We know the timestamp of the file we’re reading, but since we don’t yet know the timestamp of the other files on which the final result depends, we don’t know if we can skip this read or not. This means dependency handling should happen on a higher level, above these specific functions – so we need to abstract dependency handling.

A general notion of computation

So let’s create a wrapper for functions dealing with dependencies.

data HakyllAction a b = HakyllAction
    { actionDependencies :: [FilePath]
    , actionUrl          :: Maybe (Hakyll FilePath)
    , actionFunction     :: a -> Hakyll b
    }

Some explanation might be needed here. You can think of a as the input for our action, and then b is the output. The actionUrl contains the final destination of our computations – this can be Nothing, if it is not yet known. And finally, the actionFunction contains the actual action.

The Hakyll is a usual monad stack with IO at the bottom.

Categories

To qualify as an Arrow, a datatype needs to be a Category. So lets create an instance Category HakyllAction first. There are two functions we need to implement:

• id: The simple identity category. This is comparable to the Prelude.id function.
• .: Category composition – this is comparable to function composition.

The id action has no dependencies, no destination, and simply returns itself.

instance Category HakyllAction where
    id = HakyllAction
        { actionDependencies = []
        , actionUrl          = Nothing
        , actionFunction     = return
        }

The . action is not complicated either. The new dependencies consist of all the dependencies of the two actions. For our destination, we use an mplus with the latest applied function first, so it gets chosen over the other destination.

    x . y = HakyllAction
        { actionDependencies = actionDependencies x ++ actionDependencies y
        , actionUrl          = actionUrl x `mplus` actionUrl y
        , actionFunction     = actionFunction x <=< actionFunction y
        }

The <=< operator is right-to-left monad composition.

Arrows

To make our action a real Arrow, we need to implement two more functions:

• arr: This should lift a pure function (thus, with an a -> b signature) into HakyllAction, so we have the type signature (a -> b) -> HakyllAction a b.
• first: This is a function that should operate on one value of a tuple. This all happens “inside” HakyllAction – perhaps an illustration will explain this better. You can see how f :: a -> b applies to an (a, c) tuple, where f is applied on the first value.

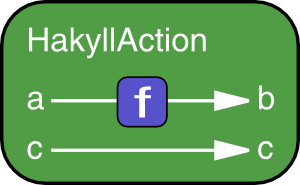
instance Arrow HakyllAction where
    arr f = id { actionFunction = return . f}
    first x = x
        { actionFunction = \(y, z) -> do
            y' <- actionFunction x y
            return (y', z)
        }

Actually using it

Now that we’ve put all this trouble into creating an Arrow, we might as well use it. Let’s examine some functions from Hakyll and see how they fit.

createPage :: FilePath -> HakyllAction () Context
render     :: FilePath -> HakyllAction Context Context
writePage  :: HakyllAction Context ()

Arrows are usually combined using the >>> operator. This gives us:

test =   createPage "contact.markdown"
     >>> render "templates/default.html"
     >>> writePage

This creates a HakyllAction but doesn’t actually do anything. We still need to run it. And now we can see the benefits of this method, since we can write a function that does dependency checking on the combined functions.

runHakyllActionIfNeeded test

The actual implementation of runHakyllActionIfNeeded goes more or less like this:

runHakyllActionIfNeeded :: HakyllAction () ()
                        -> Hakyll ()
runHakyllActionIfNeeded action = do
    url <- case actionUrl action of
        (Just u) -> u
        Nothing  -> error "At this time, an URL should be set!"
    valid <- isFileMoreRecent url $ actionDependencies action
    unless valid (actionFunction action ())

The isFileMoreRecent function checks if the first file is more recent than all of the other files.

Profit!

We have now developped a more robust and better dependency checking system, and learned something about Arrows. If you are interested, the complete code that led to this blogpost is available on here on GitHub. There are also a few other interesting things to consider:

• Can you prove the Arrows/Category laws on HakyllAction?
• Why can’t this be done using Monads?

These questions are left as an exercise to the reader. On a sidenote, kudos to BCoppens for proofreading through this post.