Stuff

Links

Tries and elegant Scope Checking

Introduction

This blogpost is mostly based upon a part of the talk I recently gave at the Haskell eXchange. I discussed scope checking – also referred to as scope analysis or renaming. While the talk focussed on Ludwig, a DSL used to program Fugue, the ideas around scope checking are broadly applicable, so in this blogpost we use a simple toy language.

{-# LANGUAGE DeriveFoldable    #-}
{-# LANGUAGE DeriveFunctor     #-}
{-# LANGUAGE DeriveTraversable #-}
import qualified Data.HashMap.Strict    as HMS
import           Data.Hashable          (Hashable)
import           Data.List              (foldl')
import           Data.Either.Validation (Validation (..),
                                         validationToEither)
import           Prelude                hiding (lookup)

This part of a Compiler/Interpreter is concerned with resolving occurence names to full names. Occurrence names are just what the programmer uses in the source file, and full names contain more information.

I think this is an interesting area to explore. The vast majority of articles about creating parsers and interpreters just use Strings as names, in order to keep things simple (which is of course fully justified). This blogpost, on the other hand, explains what you can do if things become a bit more complicated.

Consider the following Haskell snippet:

import qualified Data.HashMap.Strict as HMS

emptyThing = HMS.empty

HMS.empty is an occurrence name. The full name, on the other hand, is something like unordered-containers-0.2.5.1:Data.HashMap.Base.empty. Let’s get started by representing these types in Haskell:

-- E.g. ["HMS", "empty"].
type OccName = [String]

-- E.g. ["Data", "HashMap", "Strict"]
type ModuleName = [String]

-- Just an example of what sort of things can be in 'FullName'.
data BindingScope = ToplevelScope | LocalScope
    deriving (Show)

data FullName = FullName
    { fnOccName      :: !OccName
    , fnModuleName   :: !ModuleName
    , fnBindingScope :: !BindingScope
    } deriving (Show)

Note that this is just a toy example. Firstly, we can use more efficient representations for the above, and we might want to add newtype safety. Secondly, we might also want to store other things in FullName, for example the package where the name originated. The FullName record can really get quite big.

Now that we have two name types – OccName and FullName, we can parametrise our abstract syntax tree over a name type.

data Expr n
    = Literal Int
    | Add (Expr n) (Expr n)
    | Var n
    deriving (Show)

Now, we can formalise the problem of scope checking a bit more: it is a function which turns an Expr OccName into an Expr FullName.

Tries

In order to implement this, it is clear that we need some sort of “Map” to store the FullName information. The specific data structure we will use is a Trie. Tries are somewhat similar to Radix trees, but significantly more simple. We will implement one here for educational purposes.

A Trie k v can be seen as a mapping from lists of keys to values, so it could be defined as:

type Trie k v = HMS.HashMap [k] v

However, there is a nicer representation which we will need in order to support some fast operations.

First, we need a quick-and-dirty strict Maybe type.

data M a = J !a | N
    deriving (Foldable, Functor, Show, Traversable)

Note how we automically added Foldable, Functor and Traversable instances for this type. Thanks GHC!

Then, we can define Trie in a recursive way:

data Trie k v = Trie
    { tValue    :: !(M v)
    , tChildren :: !(HMS.HashMap k (Trie k v))
    } deriving (Foldable, Functor, Show, Traversable)

We can have a value at the root (tValue), and then the other elements in the Trie are stored under the first key of their key list (in tChildren).

Now it is time to construct some machinery to create Tries. The ¹ empty Trie is really easy:

empty :: Trie k v
empty = Trie N HMS.empty

Let’s draw the empty Trie as a simple box with an N value, since it has no value and no children.

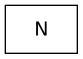
We can also define a function to create a Trie with a single element. If the list of keys is empty, we simply have a J value at the root. Otherwise, we define the function recursively.

singleton :: (Eq k, Hashable k) => [k] -> v -> Trie k v
singleton []       x = Trie (J x) HMS.empty
singleton (k : ks) x = Trie N (HMS.singleton k (singleton ks x))

As an example, this is the result of the call singleton ["foo", "bar"] "Hello World".

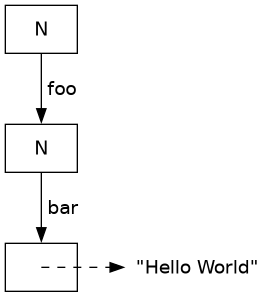
We can skip insert and simply create a unionWith function instead. This function unifies two Tries, while allowing you to pass in a function that decides how to merge the two values if there is a key collision.

unionWith
    :: (Eq k, Hashable k)
    => (v -> v -> v) -> Trie k v -> Trie k v -> Trie k v
unionWith f (Trie v1 c1) (Trie v2 c2) =
    Trie v $ HMS.unionWith (unionWith f) c1 c2
  where
    v = case (v1, v2) of
        (N,   _)   -> v2
        (_,   N)   -> v1
        (J x, J y) -> J (f x y)

The bulk of the work is of course done by HMS.unionWith. This is the result of calling unionWith (\x _ -> x) (singleton "foo" "Hello") (singleton "bar" "World"):

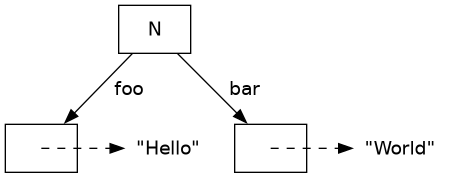
For convenience, we can then extend unionWith to work on lists:

unionsWith
    :: (Eq k, Hashable k)
    => (v -> v -> v) -> [Trie k v] -> Trie k v
unionsWith f = foldl' (unionWith f) empty

A last function we need to modify tries is prefix. This function prefixes a whole Trie by nesting it under a list of keys. Because of the way our Trie is represented, this can be done efficiently and we don’t need to change every key.

prefix :: (Eq k, Hashable k) => [k] -> Trie k v -> Trie k v
prefix []       trie = trie
prefix (k : ks) trie = Trie N $ HMS.singleton k (prefix ks trie)

This is the result of prefixing the trie from the previous example with ["qux"]:

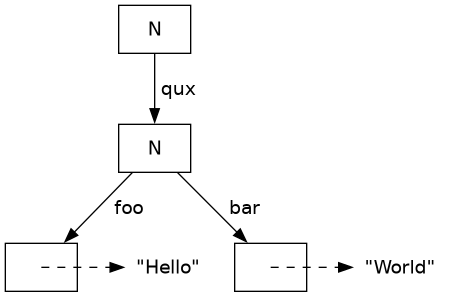
In addition to creating Tries, we also need to be able to lookup stuff in the Trie. All we need for that is a simple lookup function:

lookup :: (Eq k, Hashable k) => [k] -> Trie k v -> Maybe v
lookup []       (Trie N     _)        = Nothing
lookup []       (Trie (J x) _)        = Just x
lookup (k : ks) (Trie _     children) = do
    trie <- HMS.lookup k children
    lookup ks trie

These are all the Trie functions we need. A real implementation would, of course, offer more.

The scope type

Now, recall that we’re trying to resolve the occurrence names in a module into full names. We will tackle this from the opposite direction: we’ll gather up all the names which are in scope into one place. After this, actually, resolving an occurrence name is as simple as performing a lookup.

In order to gather up all these names we need some datatype – which is, of course, the Trie we just implemented!

type Scope a = Trie String a

We will differentiate between two different kinds of scopes (hence the a). An AmbiguousScope might contain duplicate names. In that case, we want to throw an error or show a warning to the user. In an UnambiguousScope, on the other hand, we know precisely what every name refers to.

type AmbiguousScope = Scope [FullName]
type UnambiguousScope = Scope FullName

Let’s first focus on building AmbiguousScopes. We will later see how we can validate these and convert them into an UnambiguousScope.

Building a scope for one module

In order to build a scope, let’s start with a simple case. Let’s look at a sample module in our DSL and construct a scope just for that module.

module Calories.Fruit where

apple  = 52
banana = 89

We need to have some intuition for how such a module is represented in Haskell. Let’s try to keep things as simple as possible:

data Module n = Module
    { mName     :: !ModuleName
    , mBindings :: [Binding n]
    } deriving (Show)

data Binding n = Binding
    { bName :: !n
    , bBody :: !(Expr n)
    } deriving (Show)

We can define a function to convert this module into a local Scope which contains all the bindings in the module. In order to keep things simple, we assume every binding in a module is always exported.

scopeFromModule :: Module OccName -> AmbiguousScope
scopeFromModule m =
    unionsWith (++) $ map scopeFromBinding (mBindings m)
  where
    scopeFromBinding :: Binding OccName -> AmbiguousScope
    scopeFromBinding b = singleton (bName b)
        [ FullName
            { fnOccName      = bName b
            , fnModuleName   = mName m
            , fnBindingScope = ToplevelScope
            }
        ]

For our example module, we obtain something like:

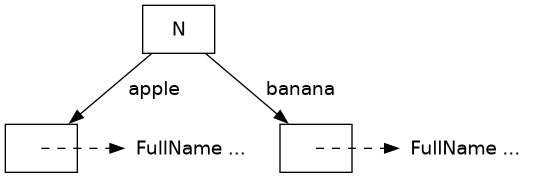
Multiple imports

Of course, a realistic program will import multiple modules. Imagine a program with the following import list:

import           Calories.Fruit
import qualified Calories.Pie  as Pie

-- An apple and an apple pie!
combo = apple + Pie.apple

In order to build the Scope for the program, we need three more things:

1. Joining a bunch of Scopes, one for each import statement (plus the local scope, and maybe a builtin scope…);
2. Qualifying a Scope, so that the qualified imports end up under the right name;
3. Finally, converting the AmbiguousScope into an UnambiguousScope.

The first one is easy, since we have our Trie machinery.

unionScopes :: [AmbiguousScope] -> AmbiguousScope
unionScopes = unionsWith (++)

So is the second:

qualifyScope :: [String] -> AmbiguousScope -> AmbiguousScope
qualifyScope = prefix

We can now build the scope for our little program. It is:

myScope :: AmbiguousScope
myScope = unionScopes
    [ scopeFromModule myModule  -- Defines 'combo'
    , scopeFromModule fruitModule
    , qualifyScope ["Pie"] $ scopeFromModule pieModule
    ]

We get something like:

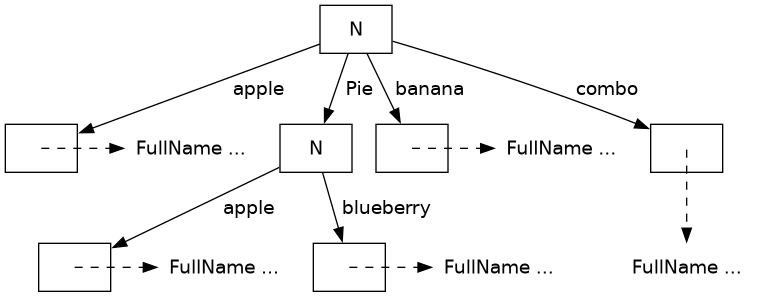
Great! So now the problem is that we’re left with an AmbiguousScope instead of an UnambiguousScope. Fortunately we can convert between those fairly easily, because Trie (and by extension Scope) is Traversable:

toUnambiguousScope
    :: AmbiguousScope -> Validation [ScopeError] UnambiguousScope
toUnambiguousScope = traverse $ \fullNames -> case fullNames of
    [single] -> pure single
    []       -> Failure [InternalScopeError "empty list in scope"]
    multiple -> Failure [AmbiguousNames multiple]

It is perhaps worth noting that this behaviour is different from GHC ².

By using the Validation Applicative, we ensure that we get as many error messages as we can. We have a nice datatype which describes our possible errors:

data ScopeError
    = AmbiguousNames [FullName]
    | NotInScope OccName
    | InternalScopeError String  -- For other failures
    deriving (Show)

Scope checking an expression

That entails everything we needed to build an UnambiguousScope, so we can now scope check a program. The actual scope checking itself is very straightforward:

scExpr
    :: UnambiguousScope -> Expr OccName
    -> Validation [ScopeError] (Expr FullName)
scExpr _ (Literal x) = pure (Literal x)
scExpr s (Add x y)   = Add <$> scExpr s x <*> scExpr s y
scExpr s (Var n)     = Var <$> scOccName s n

scOccName
    :: UnambiguousScope -> OccName
    -> Validation [ScopeError] FullName
scOccName s n = case lookup n s of
    Just fullName -> pure fullName
    Nothing       -> Failure [NotInScope n]

Conclusion

I have described a simple and (in my opinion) elegant approach to scope checking. I hope this is inspiring if you ever are in the situation where modules would be a nice extension to some DSL (or full-fledged programming language) you are implementing.

We’ve also seen how one can implement a Trie in a reasonably easy way. These often come in handy when you are modelling some sort of hierarchical Map.

This entire blogpost is written in Literate Haskell, and works as a standalone example for scope checking. If you feel up to the challenge, try to add Let-bindings as an exercise! You can find the raw .lhs file here.

Appendix

This is the rest of the source code to this blogpost, in order to make it testable (and hackable!).

fruitModule :: Module OccName
fruitModule = Module
    { mName     = ["Calories.Fruit"]
    , mBindings =
        [ Binding ["apple"]  (Literal 52)
        , Binding ["banana"] (Literal 89)
        ]
    }

pieModule :: Module OccName
pieModule = Module
    { mName     = ["Calories.Pie"]
    , mBindings =
        [ Binding ["apple"]     (Literal 240)
        , Binding ["blueberry"] (Literal 371)
        ]
    }

myModule :: Module OccName
myModule = Module
    { mName     = ["Main"]
    , mBindings =
        [ Binding ["combo"] $ Add
              (Var ["apple"])
              (Var ["Pie", "apple"])
        ]
    }

scModule
    :: UnambiguousScope -> Module OccName
    -> Validation [ScopeError] (Module FullName)
scModule s (Module n bs) = Module n <$> traverse (scBinding s) bs

scBinding
    :: UnambiguousScope -> Binding OccName
    -> Validation [ScopeError] (Binding FullName)
scBinding s (Binding n e) = Binding <$> scOccName s n <*> scExpr s e

main :: IO ()
main = do
    let ambiguous = unionScopes
          [ scopeFromModule fruitModule
          , qualifyScope ["Pie"] $ scopeFromModule pieModule
          , scopeFromModule myModule
          ]

    print $ do
        unambiguous <- validationToEither $ toUnambiguousScope ambiguous
        validationToEither $ scModule unambiguous myModule