Stuff

Links

Dynamic Graphs

TL;DR: Alex Lang and I recently “finished” a library for dealing with dynamic graphs. The library focuses on the dynamic connectivity problem in particular, although it can do some other things as well.

The story of this library began with last year’s ICFP contest. For this contest, the goal was to build a program that orchestrates a number of nanobots to build a specific minecraft-like structure, as efficiently as possible. I was in Japan at the time, working remotely from the Tsuru Capital office, and a group of them decided to take part in this contest.

I had taken part in the 2017 ICFP contest with them, but this year I was not able to work on this at all since the ICFP contest took place in the same weekend as my girlfriends’ birthday. We went to Fujikawaguchiko instead – which I would recommend to anyone interested in visiting the Fuji region. I ended up liking it more than Hakone, where I was a year or two ago.

Anyway, after the contest we were discussing how it went and Alex thought a key missing piece for them was a specific algorithm called dynamic connectivity. Because this is not a trivial algorithm to put together, we ended up using a less optimal version which still contained some bugs. In the weeks after the contest ended Alex decided to continue looking into this problem and we ended up putting this library together.

The dynamic connectivity problem is very simply explained to anyone who is at least a little familiar with graphs. It comes down to building a datastructure that allows adding and removing edges to a graph, and being able to answer the question “are these two vertices (transitively) connected” at any point in time.

This might remind you of the union-find problem. Union-find, after all, is a good solution to incremental dynamic connectivity. In this context, incremental means that edges may only be added, not removed. A situation where edges may be added and removed is sometimes referred to as fully dynamic connectivity.

Like union-find, there is unfortunately no known persistent version of this algorithm without sacrificing some performance. An attempt was made [to create a fast, persistent union find] but I don’t think we can consider this successful in the Haskell sense of purity since the structure proposed in that paper is inherently not thread-safe; which is one of the reasons to pursue persistence in the first place.

Anyway, this is why the library currently only provides a mutable interface. The library uses the PrimMonad from the primitive library to ensure you can use our code both in IO and ST, where the latter lets us reclaim purity.

Let’s walk through a simple example of using the library in plain IO.

import qualified Data.Graph.Dynamic.Levels as GD
import qualified Data.Tree                 as T

main :: IO ()
main = do
    graph <- GD.empty'

Let’s consider a fictional map of Hawaiian islands.

    mapM_ (GD.insert_ graph)
        ["Akanu", "Kanoa", "Kekoa", "Kaiwi", "Onakea"]
    GD.link_ graph "Akanu" "Kanoa"
    GD.link_ graph "Akanu" "Kaiwi"
    GD.link_ graph "Akanu" "Onakea"
    GD.link_ graph "Kaiwi" "Onakea"
    GD.link_ graph "Onakea" "Kanoa"
    GD.link_ graph "Kanoa" "Kekoa"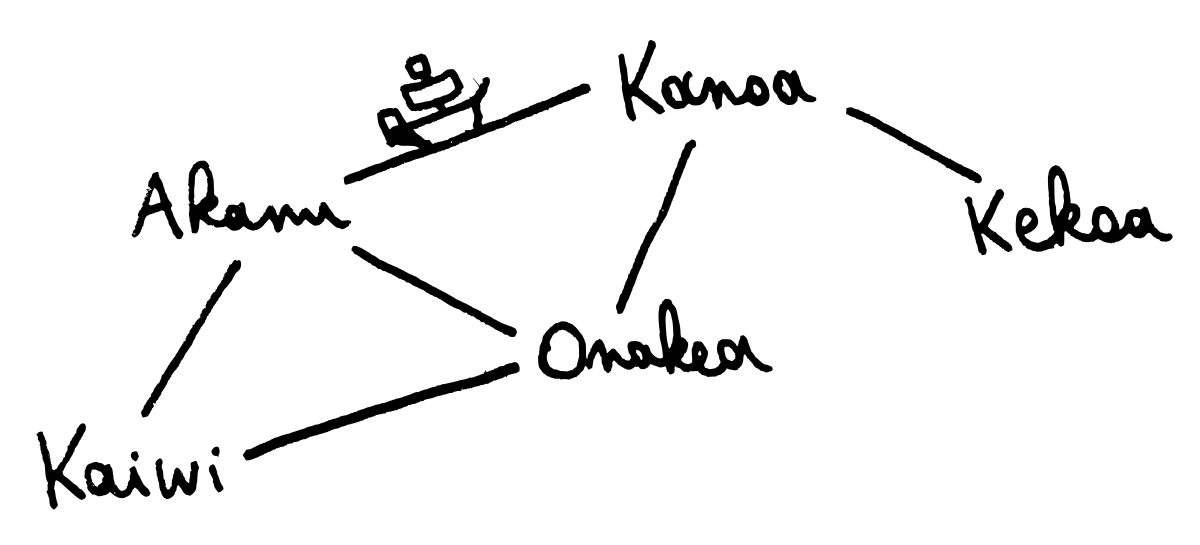

The way the algorithm works is by keeping a spanning forest at all times. That way we can quickly answer connectivity questions: if two vertices belong to the same tree (i.e., they share the same root), they are connected.

For example, can we take ferries from Kaiwi to Kekoa? The following statement prints True.

    GD.connected graph "Kaiwi" "Kekoa" >>= print

Such a question, however, could have been answered by a simpler algorithm such as union find which we mentioned before. Union find is more than appropriate if edges can only be added to a graph, but it cannot handle cases where we want to delete edges. Let’s do just so:

    GD.cut_ graph "Kaiwi" "Akanu"

In a case such as the one above, where the deleted edge is not part of the spanning forest, not much interesting happens, and the overall connectivity is not affected in any way.

However, it gets interesting when we delete an edge that is part of the spanning tree. When that happens, we kick off a search to find a “replacement edge” in the graph that can restore the spanning tree.

    GD.cut_ graph "Onakea" "Akanu"

In our example, we can replace the deleted Akanu - Onakea edge with the Kanoa - Onakea edge. Finding a replacement edge is unsurprisingly the hardest part of the problem, and a sufficiently effecient algorithm was only described in 1998 by Holm, de Lichtenberg and Thorup in this paper.

The algorithm is a little complex, but the paper is well-written, so I’ll just stick with a very informal and hand-wavey explanation here:

• If an edge is cut from the spanning forest, then this turns one spanning tree in the forest into two components.

• The algorithm must consider all edges in between these two components to find a replacement edge. This can be done be looking at the all the edges adjacent to the smaller of the two components.

• Reasonable amortized complexity, O(log² n), is achieved by “punishing” edges that are considered but not taken, so we will consider them less frequently in subsequent calls.

Back to our example. When we go on to delete the Onakea - Kanoa edge, we cannot find a replacement edge, and we are left with a spanning forest with two components.

    GD.cut_ graph "Onakea" "Kanoa"

We can confirm this by asking the library for the spanningforest and then using the very handy drawForest from Data.Tree to visualize it:

    GD.spanningForest graph >>= putStr . T.drawForest

This prints:

Kanoa
|
+- Akanu
|
`- Kekoa

Onakea
|
`- Kaiwi

Let’s restore connectivity to leave things in proper working order for the residents of our fictional island group, before closing the blogpost.

    GD.link_ graph "Akanu" "Kaiwi"

For finishing words, what are some future directions for this library? One of the authors of the original paper, M. Thorup, wrote a follow-up that improves the theoretical space and time complexity a little. This seems to punish us with bad constant factors in terms of time performance – but it is probably still worth finishing because it uses significantly less memory. Contributions, as always, are welcome. :-)