Lazy Sort: Counting Comparisons

How good is Haskell's lazy sort actually?
Published on September 17, 2020 under the tag haskell

Introduction

{-# LANGUAGE BangPatterns #-}
module Main where

import Data.IORef (IORef)
import qualified Data.Map as Map
import qualified Data.IORef as IORef
import Control.Monad (replicateM, forM_, unless, forM)
import Data.List (sort, intercalate, foldl')
import System.Random (randomIO)
import System.IO.Unsafe (unsafePerformIO)

Haskell’s laziness allows you to do many cool things. I’ve talked about searching an infinite graph before. Another commonly mentioned example is finding the smallest N items in a list.

Because programmers are lazy as well, this is often defined as:

smallestN_lazy :: Ord a => Int -> [a] -> [a]
smallestN_lazy n = take n . sort

This happens regardless of the language of choice if we’re confident that the list will not be too large. It’s more important to be correct than it is to be fast.

However, in strict languages we’re really sorting the entire list before taking the first N items. We can implement this in Haskell by forcing the length of the sorted list.

smallestN_strict :: Ord a => Int -> [a] -> [a]
smallestN_strict n l0 = let l1 = sort l0 in length l1 `seq` take n l1

If you’re at least somewhat familiar with the concept of laziness, you may intuitively realize that the lazy version of smallestN is much better since it’ll only sort as far as it needs.

But how much better does it actually do, with Haskell’s default sort?

A better algorithm?

For the sake of the comparison, we can introduce a third algorithm, which does a slightly smarter thing by keeping a heap of the smallest elements it has seen so far. This code is far more complex than smallestN_lazy, so if it performs better, we should still ask ourselves if the additional complexity is worth it.

smallestN_smart :: Ord a => Int -> [a] -> [a]
smallestN_smart maxSize list = do
    (item, n) <- Map.toList heap
    replicate n item
  where
    -- A heap is a map of the item to how many times it occurs in
    -- the heap, like a frequency counter.  We also keep the current
    -- total count of the heap.
    heap = fst $ foldl' (\acc x -> insert x acc) (Map.empty, 0) list
    insert x (heap0, count)
        | count < maxSize = (Map.insertWith (+) x 1 heap0, count + 1)
        | otherwise = case Map.maxViewWithKey heap0 of
            Nothing -> (Map.insertWith (+) x 1 heap0, count + 1)
            Just ((y, yn), _) -> case compare x y of
                EQ -> (heap0, count)
                GT -> (heap0, count)
                LT ->
                    let heap1 = Map.insertWith (+) x 1 heap0 in
                    if yn > 1
                        then (Map.insert y (yn - 1) heap1, count)
                        else (Map.delete y heap1, count)

So, we get to the main trick I wanted to talk about: how do we benchmark this, and can we add unit tests to confirm these benchmark results in CI? Benchmark execution times are very fickle. Instruction counting is awesome but perhaps a little overkill.

Instead, we can just count the number of comparisons.

Counting comparisons

We can use a new type that holds a value and a number of ticks. We can increase the number of ticks, and also read the ticks that have occurred.

data Ticks a = Ticks {ref :: !(IORef Int), unTicks :: !a}

mkTicks :: a -> IO (Ticks a)
mkTicks x = Ticks <$> IORef.newIORef 0 <*> pure x

tick :: Ticks a -> IO ()
tick t = IORef.atomicModifyIORef' (ref t) $ \i -> (i + 1, ())

ticks :: Ticks a -> IO Int
ticks = IORef.readIORef . ref

smallestN has an Ord constraint, so if we want to count the number of comparisons we’ll want to do that for both == and compare.

instance Eq a => Eq (Ticks a) where
    (==) = tick2 (==)

instance Ord a => Ord (Ticks a) where
    compare = tick2 compare

The actual ticking code goes in tick2, which applies a binary operation and increases the counters of both arguments. We need unsafePerformIO for that but it’s fine since this lives only in our testing code and not our actual smallestN implementation.

tick2 :: (a -> a -> b) -> Ticks a -> Ticks a -> b
tick2 f t1 t2 = unsafePerformIO $ do
    tick t1
    tick t2
    pure $ f (unTicks t1) (unTicks t2)
{-# NOINLINE tick2 #-}

Results

Let’s add some benchmarking that prints an ad-hoc CSV:

main :: IO ()
main = do
    let listSize = 100000
        impls = [smallestN_strict, smallestN_lazy, smallestN_smart]
    forM_ [50, 100 .. 2000] $ \sampleSize -> do
        l <- replicateM listSize randomIO :: IO [Int]
        (nticks, results) <- fmap unzip $ forM impls $ \f -> do
            l1 <- traverse mkTicks l
            let !r1 = sum . map unTicks $ f sampleSize l1
            t1 <- sum <$> traverse ticks l1
            pure (t1, r1)
        unless (equal results) . fail $
            "Different results: " ++ show results
        putStrLn . intercalate "," . map show $ sampleSize : nticks

Plug that CSV into a spreadsheet and we get this graph. What conclusions can we draw?

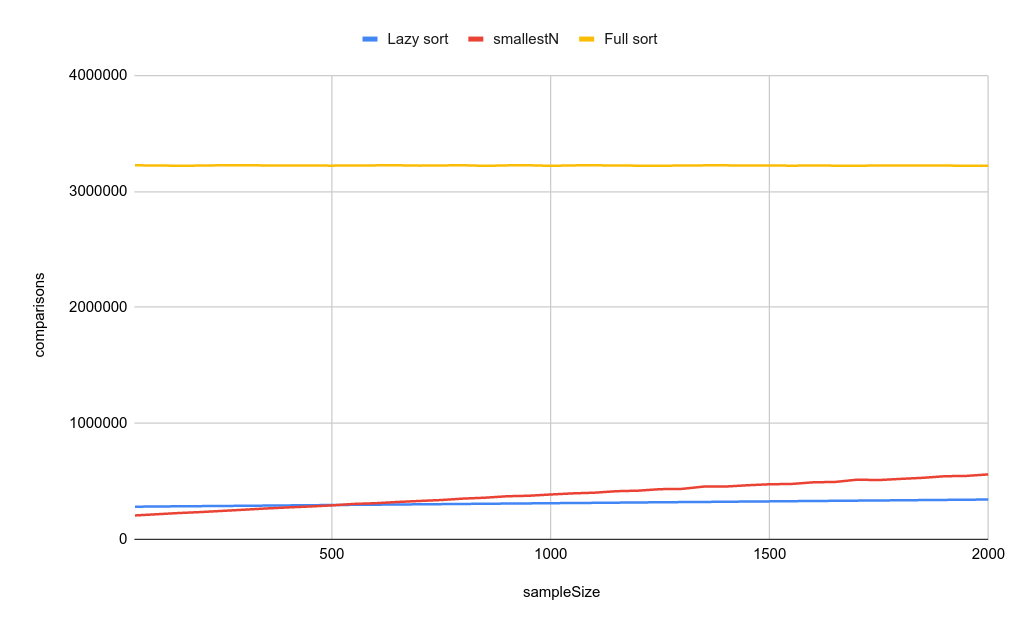
Clearly, both the lazy version as well as the “smart” version are able to avoid a large number of comparisons. Let’s remove the strict version so we can zoom in.

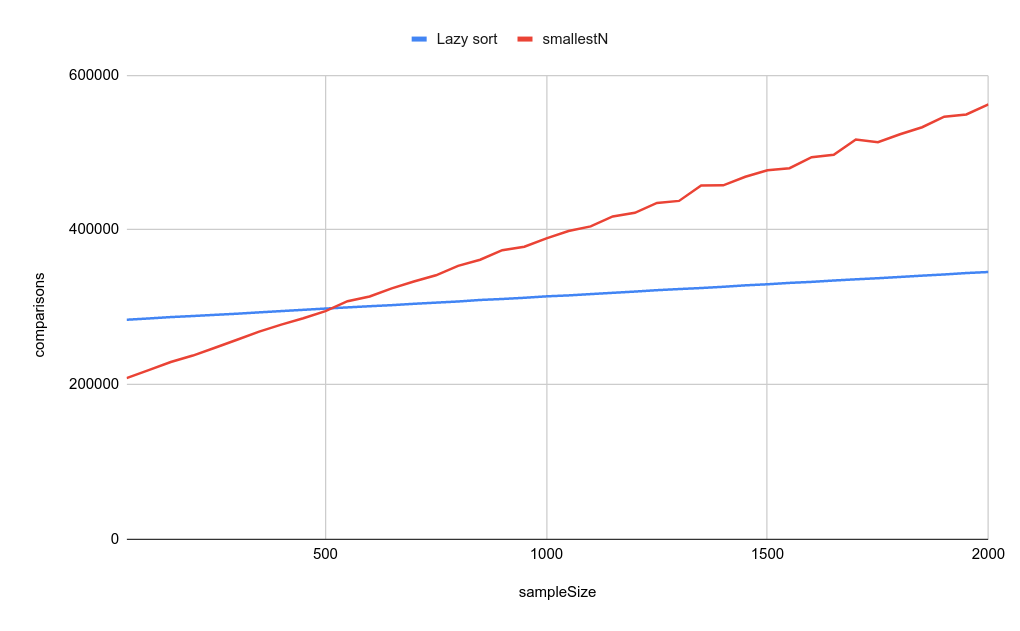
What does this mean?

Can we say something about the complexity?

Thanks to Huw Campbell for pointing out a bug in the implementation of smallestN_smart – this is now fixed in the code above.

Appendix

Helper function: check if all elements in a list are equal.

equal :: Eq a => [a] -> Bool
equal (x : y : zs) = x == y && equal (y : zs)
equal _            = True
ce0f13b2-4a83-4c1c-b2b9-b6d18f4ee6d2