Stuff

Links

The Dwarfs and The Fast Marking Algorithm

The problem

In a far away mountain, there was a large dwarven colony. At the time when this story took place, not a lot of dwarfs still lived there, though. The dwarven complex was huge, full of dark corridors, hidden tunnels and no longer used rooms. The dwarfs that were left, lived in a small number of rooms deep inside the complex.

But legends say that a lot of treasures, long forgotten, remained hidden in a handful of the supposedly 20,000 rooms making up the complex. Due to the massiveness of the complex, it was an impossible task for the dwarfs to search all rooms, so they sent out random expeditions.

A naive solution

Being with so few, the dwarfs did not want to visit a room twice, for their time was too valuable. So, they wanted a computer program with which they could mark the rooms they have already been to. One of the younger dwarfs quickly came up with a solution.

However, the dwarven council was not pleased with this solution. The young dwarf had used Java (the older dwarfs really don’t like Java), but aside from that, the older dwarfs quickly found out that the algorithm would run in O(n) time, with n being the total number of rooms in the complex (20,000).

“Indeed,” the young dwarf spoke, “the algorithm will take O(n) to initialize the marks array”. “We can’t have that,” the dwarven council answered, “we have too many rooms and too little time.”

For completeness reasons, here was the simple code that the young dwarf had written:

public class Marker {
    private boolean[] marks;

    public Marker(int size) {
        marks = new boolean[size];
    }

    public void mark(int index) {
        marks[index] = true;
    }

    public boolean isMarked(int index) {
        return marks[index];
    }
}

Abusing malloc’s complexity

One of the older dwarven lords then spoke, wise as he was: “This is inherent to Java – you should try to use C. malloc will run in O(1), and this will solve the problem.”

The young dwarf shoke his head, speaking “You ask me to do the impossible. If the array is not initialized – and thus filled with random elements – we cannot know if a mark has been set! If you think this can be done, why don’t you show it to us?”

The dwarven lord spoke again “It is possible, but I am far too old to be kept busy with these kind of problems – I suggest you think it over again, it is not very hard, and it will be a good exercise.”

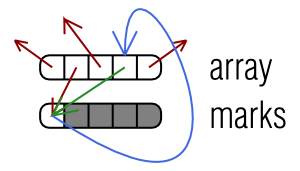
The solution

The solution of the dwarven lord goes a bit like this: two arrays of the requested size are allocated. We shall call one array and the other one marks. They are both filled with random elements, since we do not want to initialize them.

The array can be compared to the array used in the Java program, except all values are initially random integers.

In addition to the marks array, we keep the number of marks set. Initially, this number is 0. All values in the marks array are random integers, too.

When we want to mark an item, instead of setting the corresponding element of array to true, we let it point to the next position in marks and we increment the number of marks. Now, we have this element in marks point back to the element in array. This way, an element in array can, by chance, point to an element in marks, but this won’t matter since the element in marks won’t point back, and so we can determine it’s fake.

This figure illustrates the algorithm. Only one element is marked: the fourth element. Therefore, only one element from the marks structure is used (the number is set to 1). All elements in the array except the fourth element point to random positions. The fourth points to the first mark (since we set the fourth mark).

By chance, the second element in array also points to the first mark. However, we can easily see that only the fourth element is marked, since the first mark points back to the fourth element in array.

Here is an implementation in C.

Trivia

Thanks to Denis Defreyne for proofreading this blogpost, and Gunnar Brinkmann for the problem suggestion. The dwarf images were taken from The Battle for Wesnoth.

Update

Since there’s been a lot of comments, here is a small update.

First off, this algorithm will never return an incorrect result. There will be no false positives nor false negatives.

Now, on the complexity. The time complexity is roughly the same as for most set implementations (hashset, treeset): O(1) initialization, O(1) add/contains and O(m) traversal (with m the number of elements in the set, not the size of the universe). The benefit of this approach (in comparison to a classic set implementation) is that the constant factors will be a lot better. The disadvantage is that it uses a lot of memory. Another disadvantage is that you can only use this approach when you can consecutively number the elements in the universe.